【QA】邏輯斯迴歸(logistic regression)? - Cupoy

2021/10/03 下午 11:18

機器學習共學討論版

Ray

觀看數：99

回答數：1

收藏數：1

回答列表

• 2021/10/03 下午 11:23
  Ray
  贊同數：0
  不贊同數：0
  留言數：0

  邏輯斯迴歸(logistic regression)是十分容易實作的分類模型，能夠處理線性以及二元的分類問題，並且當資料是可被線性分類的狀況下表現非常好，同時也是在業界被廣泛使用的分類演算法之一，一開始我們先以圖示的方式去簡單了解邏輯斯迴歸(logistic regression)的分類方法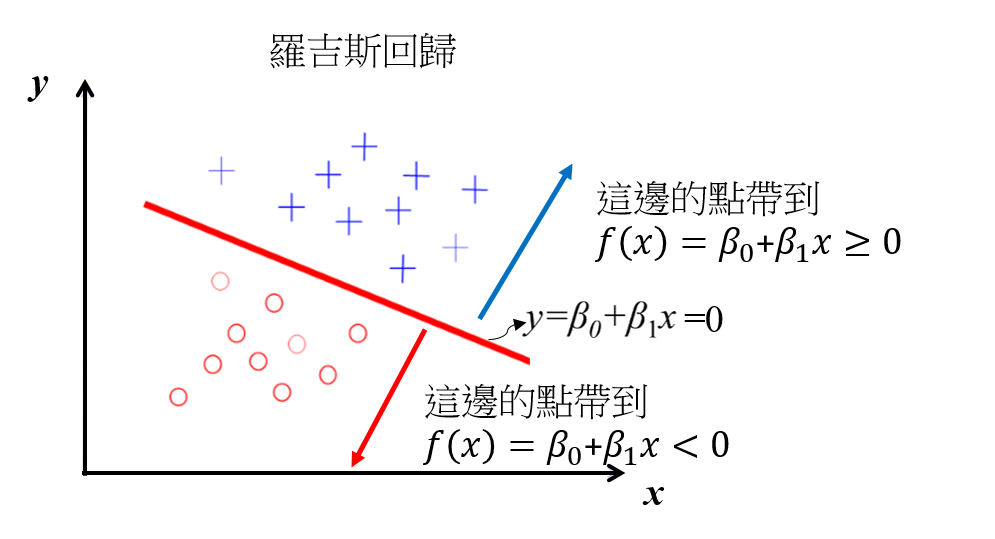： [參考圖片來源](https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8-%E7%B5%B1%E8%A8%88%E5%AD%B8%E7%BF%92-%E7%BE%85%E5%90%89%E6%96%AF%E5%9B%9E%E6%AD%B8-logistic-regression-aff7a830fb5d) 將樣本的值帶入回歸線中，大於0則屬於上方的那一類，小於0則屬於下方那一類，這便是邏輯斯迴歸(logistic regression)最簡單的分類方法，但是這種方法過於直接、簡單，難以實際應用，因此我們便要講到其中的對數函數了，在此之前我們先介紹一下勝算比(odds ratio)，它指的是對特定事件出現的比率。勝算比可以寫成p/(1-p)，其中p代表正事件(positive event）的機率，正事件(positive event）指的是我們所要預測的目標；接著我們可以進一步定義logit函數，這是勝算比的對數結果，也稱為『對數勝算(log-odds)』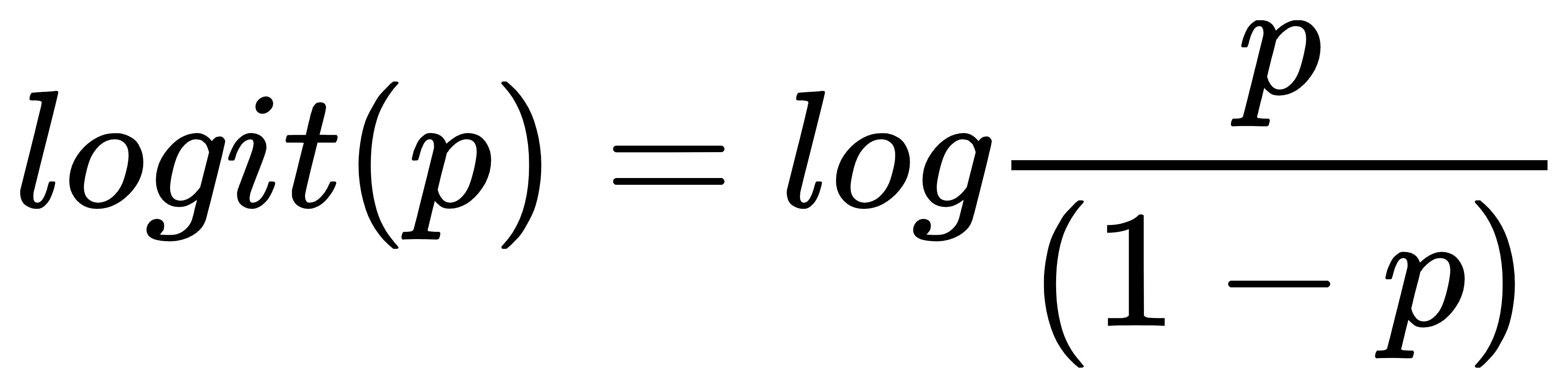：  函數logit的輸入為0到1之間的值，logit函數會將輸入轉換為分布於整個實數範圍內的值，我們可以用它來表示特徵值與勝算比之間的線性關係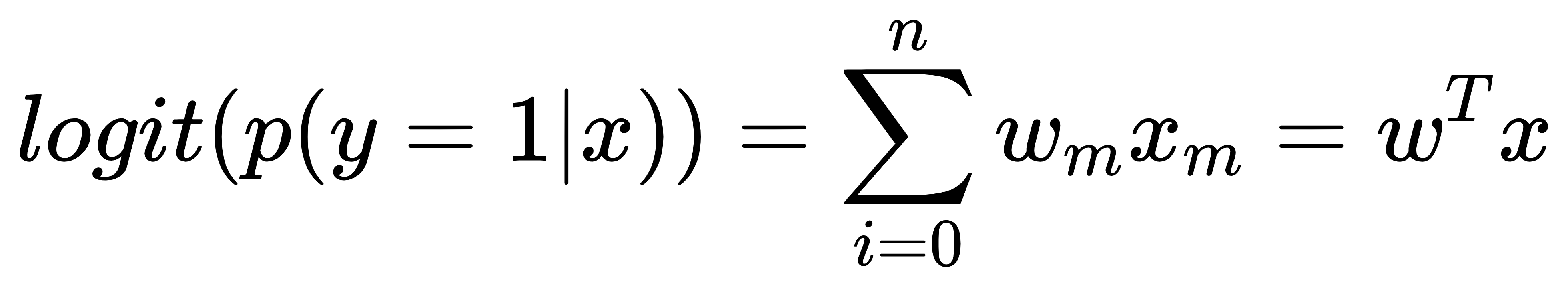：  這邊的p(y=1|x)是指給定特徵x時，當特定樣本屬於正事件(positive event）類別的條件機率；講到這邊不知各位是否有注意到，在logt函數中的輸入才是我們所需要的，預測特定樣本在特定類別中的機率，因此我們真正需要關心的是logit函數的反函數，又稱為logistic函數，他有另外一個各位可能較為熟悉的名字－sigmoid函數。 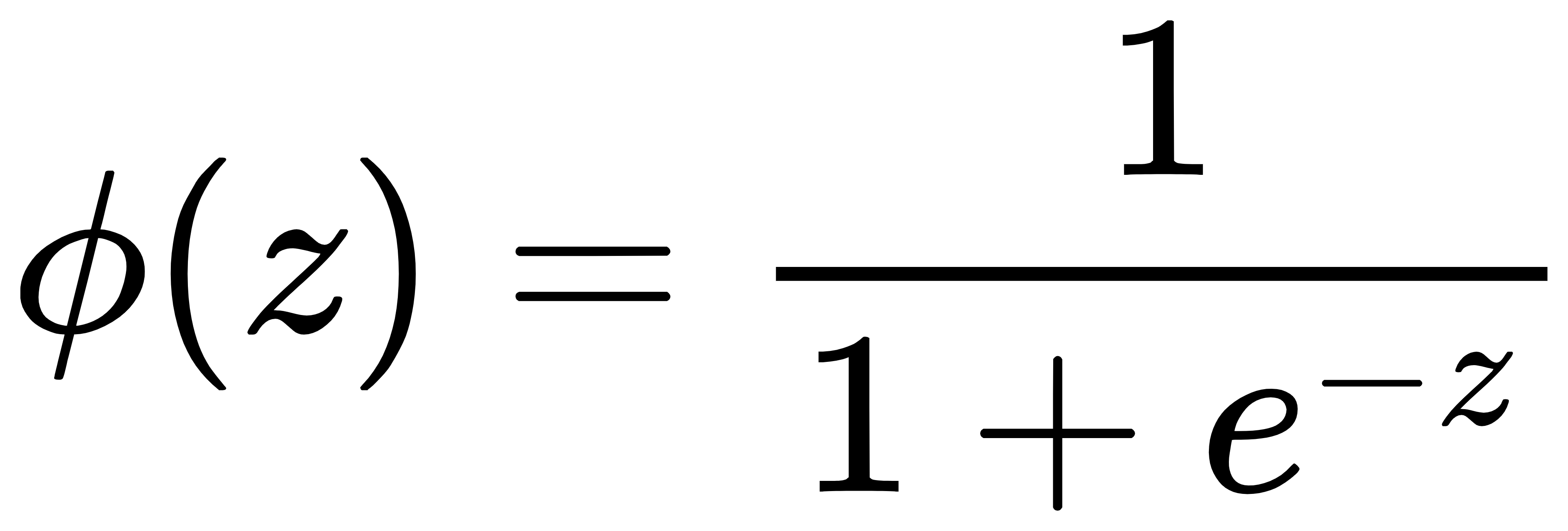 這裡的z指的是淨輸入，也就是權重以及樣本特徵的線性組合，其方程式如下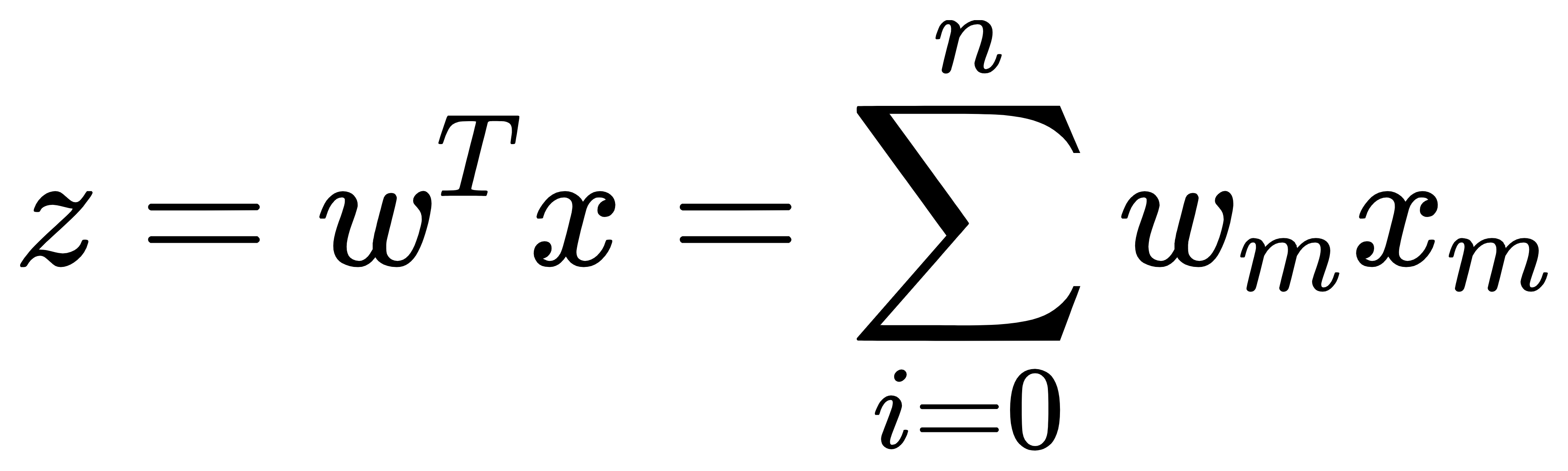：  ------------------------- 有興趣進一步了解的人可參考以下連結： * [機器/統計學習: 羅吉斯回歸(Logistic regression)](https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8-%E7%B5%B1%E8%A8%88%E5%AD%B8%E7%BF%92-%E7%BE%85%E5%90%89%E6%96%AF%E5%9B%9E%E6%AD%B8-logistic-regression-aff7a830fb5d) * [Logistic Regression 介紹 ](https://cchia.kmu.edu.tw/images/%E6%96%87%E7%AB%A0/2-Logistic_Regression_%E4%BB%8B%E7%B4%B9.pdf) * [[機器學習首部曲] 邏輯斯迴歸模型 Logistic Regression](https://pyecontech.com/2020/01/04/logistic_regression/)