【QA】什麼是Information Entropy ??
資訊量看似很抽象的概念,實則是可被量化計算的,而information entroy 就是資訊度量的計算規則,也在之後被用於機器學習當中,作為常用的損失函數,下面我想跟大家討論一下,資料量計算的方式。
回答列表
-
2021/09/01 下午 04:39Chili贊同數:0不贊同數:0留言數:0
* 資訊量(Information)的定義:消息數的對數 (底數為2) (假設每個消息產生的可能性相同,並有m種消息信源) 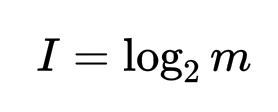 舉一個簡單的例子來說明,假設有一枚硬幣,正面、反面出現的機率皆為0.5,則m=2。 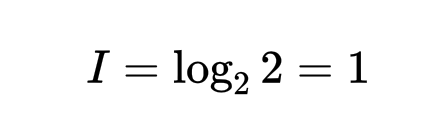 訊息量為1 bit --- 而在一般生活中,常見的事件不易引起大家的注目,反而是出現一件反常新聞時,才容易引起大家的關注(surprise),也就是說,發生機率小的事件,帶來的訊息量比較大,常見的事件帶給我們訊息量比較小,因此我們可以定義公式為: 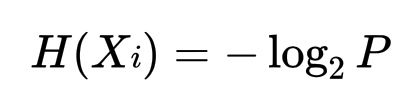 *Xi 代表一個事件發生,P為該事件發生的機率 --- 假設過去丟64次硬幣的情況為,63次正面,1次反面,那麼63/64會被認為是正面的機率,也就是P。 * 如果下一次丟硬幣,仍為正面時,所帶來的資訊量是 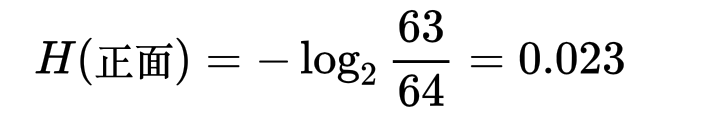 * 為反面時,所帶來的資訊量是 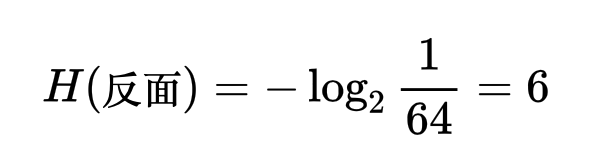 我們可以發現到發生機率比較小的事件發生時所帶來的資訊量比較大。 --- * 資訊熵(information entropy): 所謂的資訊熵就是“資訊雜亂程度的量化”,公式為 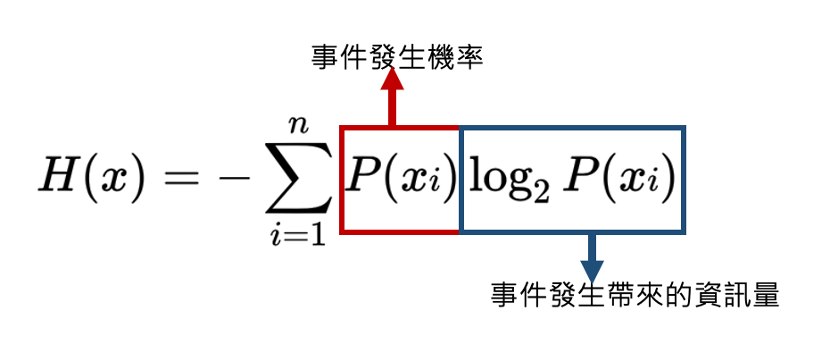 若個事件X發生的事件產生的機率乘上該事件帶來的資訊量,並最後做加總。 --- * 當硬幣正面、反面出現機率大不相同時: (正面出現機率極高) 下一次丟硬幣結果資訊熵為0.1166 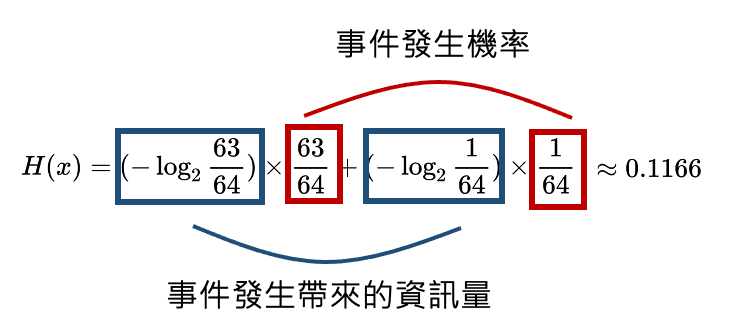 --- * 當硬幣正面、反面出現機率相同時: 下一次丟硬幣結果資訊熵為1 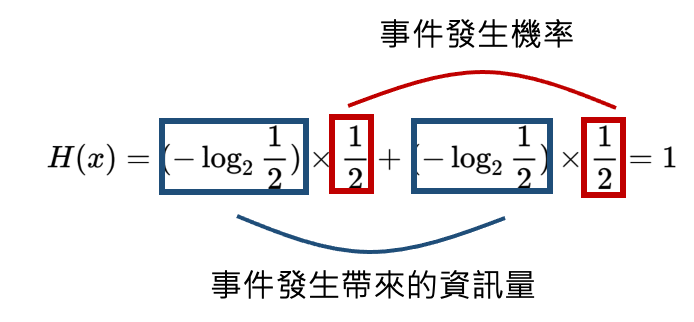 --- * 從上述兩個情況可以看出: 資料越確定,事件出現機率大不相同時,情況越單一,資訊熵越小。 (下一次出現正面的機率極高) 資料越不確定,事件出現機率相同時,情況越複雜,資訊熵越大。 (下一次出現正面的機率與出現反面機率相同) --- * 參考資料: 詳細影片解釋cross entropy的計算: https://statquest.org/entropy-for-data-science-clearly-explained/ https://chih-sheng-huang821.medium.com/機器-深度學習-基礎介紹-損失函數-loss-function-2dcac5ebb6cb https://arbu00.blogspot.com/2018/01/10.html
