【QA】如何用決策樹(Decision Tree)做Bagging?
Bagging是Ensemble learning(集成學習)的一種方法,本次想就如何用決策樹做Bagging來進行討論
回答列表
-
2021/08/15 下午 09:39Ray贊同數:1不贊同數:0留言數:0
在開始之前,我們先大致了解一下Bagging的概念,Bagging的概念很簡單,就是從N筆訓練資料中隨機抽取n個(取出後放回,通常n=N)樣本建立dataset,然後訓練多個分類器(要多少個分類器自己設定),每個分類器的權重一致最後用投票方式(Majority vote)得到最終結果,而這種抽樣的方法在統計上稱為bootstrap。 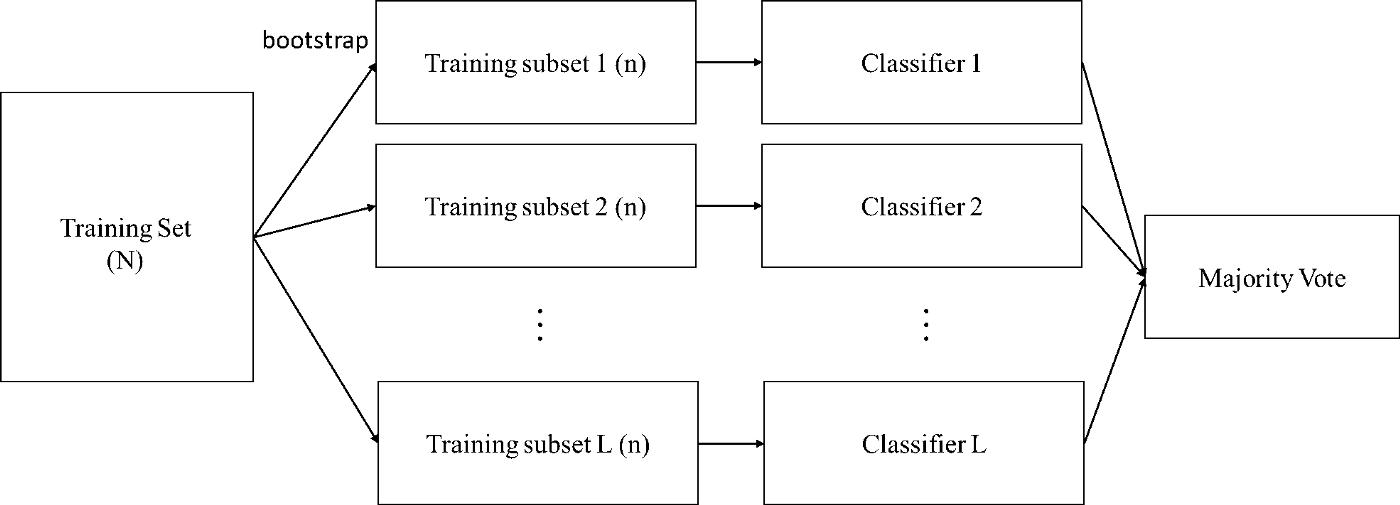 若要使用決策樹做Bagging的話,就必須要提到隨機森林了,隨機森林是Bagging的一個擴充套件變體,隨機森林在以決策樹為基分類器構建Bagging整合的基礎上,進一步在決策樹的訓練過程中加入了隨機屬性選擇,也就是從所有屬性中隨機選擇k個屬性,然後選擇最佳分割屬性作為節點建立CART決策樹;重複以上兩個步驟m次,即建立了m棵CART決策樹,這m棵CART決策樹會形成隨機森林,最後通過投票表決結果,決定資料屬於哪一類 有興趣進一步了解Bagging的人可以參考該[連結](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.BaggingClassifier.html#sklearn.ensemble.BaggingClassifier) 以下用實際例子來進一步進行說明 描述:輸入的特徵是二維的,紅色的部分是class1,藍色的部分是class2,其中class1分佈的和初音的樣子是一樣的。我們用決策樹對這個問題進行分類。  決策樹實驗結果: 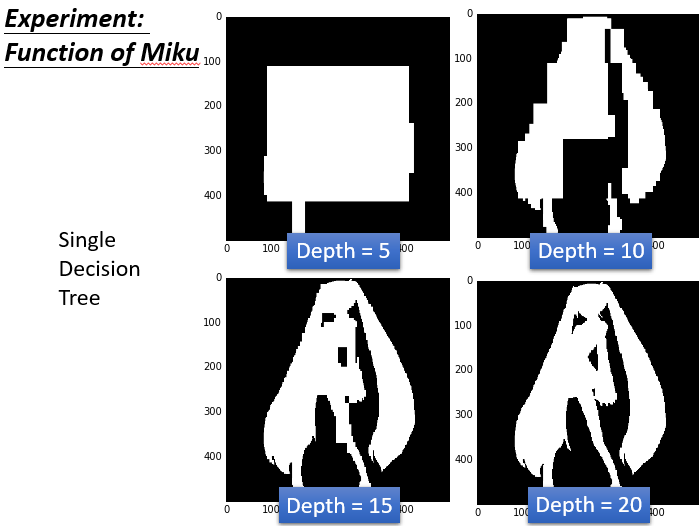 上圖可以看到,深度是5的時候效果並不好,圖中白色的就是class1,黑色的是class2.當深度是10的時候有一點初音的樣子,當深度是15的時候,基本初音的輪廓就出來了,但是一些細節還是很奇怪(比如一些凸起來的邊角)當深度是20的時候,就可以完美的把class1和class2的位置區別開來,就可以完美地把初音的樣子勾勒出來了。對於決策樹,理想的狀況下可以達到錯誤是0的時候,最極端的就是每一筆data point就是很深的樹的一個節點,這樣正確率就可以達到100%(樹夠深,決策樹可以做出任何的function)但是決策樹很容易過擬合,如果只用決策樹一般很難達到好的結果。  用決策樹做Bagging就是隨機森林傳統的隨機森林是通過之前的重採樣的方法做,但是得到的結果是每棵樹都差不多(效果並不好)。比較多的是隨機的限制一些特徵或者問題不能用,這樣就能保證就算用同樣的dataset,每次產生的決策樹也會是不一樣的,最後把所有的決策樹的結果都集合起來,就會得到隨機森林。如果是用Bagging的方法的話,用out-of-bag可以做驗證。用這個方法可以不用把label data劃分成training set和validation set,一樣能得到同樣的效果。具體做法:假設我們有training data是x^1,x^2,x^3,x^4,f1我們只用第一筆和第二筆data訓練(圓圈表示訓練,叉表示沒訓練),f2我們只用第三筆第四筆data訓練,f3用第一,第三筆data訓練,f4表示用第二,第四筆data訓練,我們知道,在訓練f1和f4的時候沒有用到x^1,所以我們就可以用f1和f4 Bagging的結果在x^1上面測試他們的表現,同理,我們可以用f2和f3 Bagging的結果來測試x^2下面幾個也是同樣的道理。最後用把每個測試的結果取平均的error,就作為最後的error。雖然我們沒有明確的切出一個驗證集,但是我們做測試的時候所有的模型並沒有看過那些測試的數據。所有這個輸出的error也是可以作為反映測試集結果的估測效果。 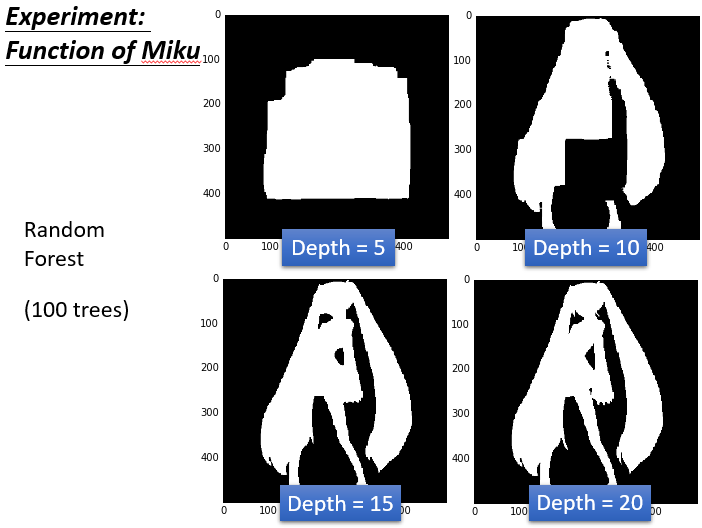 強調一點是做Bagging更不會使模型能fit data,所有用深度為5的時候還是不能fit出一個function,所有就是5顆樹的一個平均,相當於得到一個比較平滑的樹。當深度是10的時候,大致的形狀能看出來了,當15的時候效果就還不錯,但是細節沒那麼好,當20 的時候就可以完美的把初音分出來。 **隨機森林的優點:** 1. 表現效能好,與其他演算法相比有著很大優勢。 2. 隨機森林能處理很高維度的資料(也就是很多特徵的資料),並且不用做特徵選擇。 3. 在訓練完之後,隨機森林能給出哪些特徵比較重要。 4. 訓練速度快,容易做成並行化方法(訓練時,樹與樹之間是相互獨立的)。 5. 在訓練過程中,能夠檢測到feature之間的影響。 6. 對於不平衡資料集來說,隨機森林可以平衡誤差。當存在分類不平衡的情況時,隨機森林能提供平衡資料集誤差的有效方法。 7. 如果有很大一部分的特徵遺失,用RF演算法仍然可以維持準確度。 8. 隨機森林演算法有很強的抗干擾能力(具體體現在6,7點)。所以當資料存在大量的資料缺失,用RF也是不錯的。 9. 隨機森林抗過擬合能力比較強(雖然理論上說隨機森林不會產生過擬合現象,但是在現實中噪聲是不能忽略的,增加樹雖然能夠減小過擬合,但沒有辦法完全消除過擬合,無論怎麼增加樹都不行,再說樹的數目也不可能無限增加的。) 10. 隨機森林能夠解決分類與迴歸兩種型別的問題,並在這兩方面都有相當好的估計表現。(雖然RF能做迴歸問題,但通常都用RF來解決分類問題)。 11. 在建立隨機森林時候,對generlization error(泛化誤差)使用的是無偏估計模型,泛化能力強。 **隨機森林的缺點:** 1. 隨機森林在解決迴歸問題時,並沒有像它在分類中表現的那麼好,這是因為它並不能給出一個連續的輸出。當進行迴歸時,隨機森林不能夠做出超越訓練集資料範圍的預測,這可能導致在某些特定噪聲的資料進行建模時出現過度擬合。(PS:隨機森林已經被證明在某些噪音較大的分類或者回歸問題上回過擬合)。 2. 對於許多統計建模者來說,隨機森林給人的感覺就像一個黑盒子,你無法控制模型內部的執行。只能在不同的引數和隨機種子之間進行嘗試。如果有興趣了解如何解釋隨機森林的結果的人可參考該[連結](https://www.analyticsvidhya.com/blog/2019/08/decoding-black-box-step-by-step-guide-interpretable-machine-learning-models-python/?utm_source=blog&utm_medium=decision-tree-vs-random-forest-algorithm) 3. 可能有很多相似的決策樹,掩蓋了真實的結果。 4. 對於小資料或者低維資料(特徵較少的資料),可能不能產生很好的分類。(處理高維資料,處理特徵遺失資料,處理不平衡資料是隨機森林的長處)。 5. 執行資料雖然比boosting等快(隨機森林屬於bagging),但比單隻決策樹慢多了。 (fc>#ff0000:注意:隨機森林不一定是由決策樹作為基分類器,習慣上由SVM、邏輯回歸等分類器組成的總分類器也稱為隨機森林。
